La onda periódica más simple: una onda armónica. En este ejemplo, A=1, Ω=1 y θ=0.
Las ondas periódicas son aquellas ondas que muestran periodicidad respecto del tiempo, es decir, describen ciclos repetitivos. En una onda periódica se cumple:
donde el periodo propio fundamental 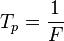 ,
,  es la frecuencia de la componente fundamental de la onda periódica y
es la frecuencia de la componente fundamental de la onda periódica y
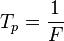 ,
,  es la frecuencia de la componente fundamental de la onda periódica y
es la frecuencia de la componente fundamental de la onda periódica y Toda onda periódica es, por definición, una onda determinista, por cuanto puede ser descrita matemáticamente (mediante un modelo matemático).
La forma más simple de onda periódica es la onda armónica (sinusoidal), que se describe matemáticamente:

Esta onda está completamente caracterizada por tres parámetros:  es la amplitud de la sinusoide,
es la amplitud de la sinusoide, 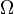 es la frecuencia en radianes por segundo (rad/s), y
es la frecuencia en radianes por segundo (rad/s), y 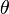 es la fase en radianes. En lugar de
es la fase en radianes. En lugar de 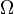 , a menudo se utiliza la frecuencia
, a menudo se utiliza la frecuencia  ciclos por segundo o hercios (Hz), donde
ciclos por segundo o hercios (Hz), donde  .
.
siendo el número total de armónicos de los que se compone la onda periódica. El armónico de frecuencia más baja se denomina primer armónico o armónico de frecuencia fundamental (
el número total de armónicos de los que se compone la onda periódica. El armónico de frecuencia más baja se denomina primer armónico o armónico de frecuencia fundamental ( , por tanto de amplitud
, por tanto de amplitud  , frecuencia
, frecuencia 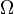 y fase
y fase 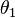 ). De hecho, el caso más simple, el de una onda armónica, es un caso particular para un único armónico (
). De hecho, el caso más simple, el de una onda armónica, es un caso particular para un único armónico ( ). Otros casos requieren un número infinito de armónicos que sólo pueden existir en sus formas perfectas como abstracciones matemáticas debido a que en la naturaleza no se pueden crear o transmitir señales de ancho de banda infinito. Sin embargo, incluso sus aproximaciones (descritos como la suma de un número limitado de armónicos) son de gran interés en la práctica, especialmente en Telecomunicaciones. Entre estos casos de señales periódicas compuestos por infinitos armónicos se encuentran las ondas cuadradas (onda compuesta exclusivamente por armónicos impares cuya amplitud es inversamente proporcional al número de armónico, es decir,
). Otros casos requieren un número infinito de armónicos que sólo pueden existir en sus formas perfectas como abstracciones matemáticas debido a que en la naturaleza no se pueden crear o transmitir señales de ancho de banda infinito. Sin embargo, incluso sus aproximaciones (descritos como la suma de un número limitado de armónicos) son de gran interés en la práctica, especialmente en Telecomunicaciones. Entre estos casos de señales periódicas compuestos por infinitos armónicos se encuentran las ondas cuadradas (onda compuesta exclusivamente por armónicos impares cuya amplitud es inversamente proporcional al número de armónico, es decir, ![x_a(t) = \frac {4A}{\pi} \sum_{n=1}^\infty \frac {1}{2n-1} \sin [(2n-1) \Omega t +\theta] \,\!](http://upload.wikimedia.org/math/c/2/9/c29b0e122721152e7d58af2f2996e638.png) ) o las triangulares.
) o las triangulares.
Esta propiedad demostrada por Fourier sobre las ondas periódicas es importante en el estudio de la Teoría de la Información y, muy especialmente, en la demostración del Teorema de muestreo de Nyquist-Shannon. Este teorema demuestra que toda onda periódica limitada en banda (limitada a componentes armónicos por debajo de una frecuencia máxima conocida) puede ser descrita en su totalidad y sin ambigüedad por una serie de muestras no cuantificadas si se cumple que la frecuencia de muestreo es superior (nunca igual) al doble de la frecuencia del último armónico que puede contener la onda.
 es la amplitud de la sinusoide,
es la amplitud de la sinusoide, 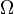 es la frecuencia en radianes por segundo (rad/s), y
es la frecuencia en radianes por segundo (rad/s), y 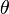 es la fase en radianes. En lugar de
es la fase en radianes. En lugar de 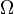 , a menudo se utiliza la frecuencia
, a menudo se utiliza la frecuencia  ciclos por segundo o hercios (Hz), donde
ciclos por segundo o hercios (Hz), donde  .
. El proceso de determinación matemática de los coeficientes  y las constantes de fase
y las constantes de fase  , para una forma de onda dada se llama análisis de Fourier. Al igual que una forma de onda periódica puede analizarse como una serie de Fourier mediante las contribuciones relativas de la frecuencia fundamental y los armónicos superiores presentes en la forma de onda, también es posible construir nuevas formas de onda periódicas, sumando a la frecuencia fundamental distintas contribuciones de sus armónicos superiores. Este proceso se denomina síntesis de Fourier.
, para una forma de onda dada se llama análisis de Fourier. Al igual que una forma de onda periódica puede analizarse como una serie de Fourier mediante las contribuciones relativas de la frecuencia fundamental y los armónicos superiores presentes en la forma de onda, también es posible construir nuevas formas de onda periódicas, sumando a la frecuencia fundamental distintas contribuciones de sus armónicos superiores. Este proceso se denomina síntesis de Fourier.
 y las constantes de fase
y las constantes de fase  , para una forma de onda dada se llama análisis de Fourier. Al igual que una forma de onda periódica puede analizarse como una serie de Fourier mediante las contribuciones relativas de la frecuencia fundamental y los armónicos superiores presentes en la forma de onda, también es posible construir nuevas formas de onda periódicas, sumando a la frecuencia fundamental distintas contribuciones de sus armónicos superiores. Este proceso se denomina síntesis de Fourier.
, para una forma de onda dada se llama análisis de Fourier. Al igual que una forma de onda periódica puede analizarse como una serie de Fourier mediante las contribuciones relativas de la frecuencia fundamental y los armónicos superiores presentes en la forma de onda, también es posible construir nuevas formas de onda periódicas, sumando a la frecuencia fundamental distintas contribuciones de sus armónicos superiores. Este proceso se denomina síntesis de Fourier.Es importante notar que para las señales de ancho de banda limitado (en la práctica, todas las de interés en Telecomunicaciones), la suma de armónicos es también finita:

siendo
 el número total de armónicos de los que se compone la onda periódica. El armónico de frecuencia más baja se denomina primer armónico o armónico de frecuencia fundamental (
el número total de armónicos de los que se compone la onda periódica. El armónico de frecuencia más baja se denomina primer armónico o armónico de frecuencia fundamental ( , por tanto de amplitud
, por tanto de amplitud  , frecuencia
, frecuencia 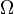 y fase
y fase 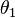 ). De hecho, el caso más simple, el de una onda armónica, es un caso particular para un único armónico (
). De hecho, el caso más simple, el de una onda armónica, es un caso particular para un único armónico ( ). Otros casos requieren un número infinito de armónicos que sólo pueden existir en sus formas perfectas como abstracciones matemáticas debido a que en la naturaleza no se pueden crear o transmitir señales de ancho de banda infinito. Sin embargo, incluso sus aproximaciones (descritos como la suma de un número limitado de armónicos) son de gran interés en la práctica, especialmente en Telecomunicaciones. Entre estos casos de señales periódicas compuestos por infinitos armónicos se encuentran las ondas cuadradas (onda compuesta exclusivamente por armónicos impares cuya amplitud es inversamente proporcional al número de armónico, es decir,
). Otros casos requieren un número infinito de armónicos que sólo pueden existir en sus formas perfectas como abstracciones matemáticas debido a que en la naturaleza no se pueden crear o transmitir señales de ancho de banda infinito. Sin embargo, incluso sus aproximaciones (descritos como la suma de un número limitado de armónicos) son de gran interés en la práctica, especialmente en Telecomunicaciones. Entre estos casos de señales periódicas compuestos por infinitos armónicos se encuentran las ondas cuadradas (onda compuesta exclusivamente por armónicos impares cuya amplitud es inversamente proporcional al número de armónico, es decir, ![x_a(t) = \frac {4A}{\pi} \sum_{n=1}^\infty \frac {1}{2n-1} \sin [(2n-1) \Omega t +\theta] \,\!](http://upload.wikimedia.org/math/c/2/9/c29b0e122721152e7d58af2f2996e638.png) ) o las triangulares.
) o las triangulares.Esta propiedad demostrada por Fourier sobre las ondas periódicas es importante en el estudio de la Teoría de la Información y, muy especialmente, en la demostración del Teorema de muestreo de Nyquist-Shannon. Este teorema demuestra que toda onda periódica limitada en banda (limitada a componentes armónicos por debajo de una frecuencia máxima conocida) puede ser descrita en su totalidad y sin ambigüedad por una serie de muestras no cuantificadas si se cumple que la frecuencia de muestreo es superior (nunca igual) al doble de la frecuencia del último armónico que puede contener la onda.
Sin embargo, el modelo descrito para las ondas armónicas no sirve para describir estructuras periódicas más complicadas: las ondas anarmónicas. Joseph Fourier demostró que las ondas periódicas con formas complicadas pueden considerarse como suma de ondas armónicas (cuyas frecuencias son siempre múltiplos enteros de la frecuencia fundamental). Así, supongamos que  representa el desplazamiento periódico de una onda en una cierta posición. Si
representa el desplazamiento periódico de una onda en una cierta posición. Si  y su derivada son continuas, puede demostrarse que dicha función puede representarse mediante una suma del tipo:
y su derivada son continuas, puede demostrarse que dicha función puede representarse mediante una suma del tipo:
 representa el desplazamiento periódico de una onda en una cierta posición. Si
representa el desplazamiento periódico de una onda en una cierta posición. Si  y su derivada son continuas, puede demostrarse que dicha función puede representarse mediante una suma del tipo:
y su derivada son continuas, puede demostrarse que dicha función puede representarse mediante una suma del tipo:



![x_a(t) = \frac {4A}{\pi} \sum_{n=1}^{25} \frac {1}{2n-1} \sin [(2n-1) \Omega t +\pi] \,\!](http://upload.wikimedia.org/math/2/7/7/2770309267ccc66cd37eaa9d525de857.png)

este tema la verdad nunca lo había leido, esta muy vistozo me gusto mucho los movimientos de las ondas, las formulas son muy explicitas y muy bien despejadas, las ondas períodicas que muestran periocidad respecto al tiempo. Acerca de los nodos que ya sabia que eran pero los entendi con mayor claridad.
ResponderEliminarMireya Rosas 5B
el tema de los nodos y antinodos no esta muy completo porque viene en ingles y la mayoria de las personas no lo van a entender, les recomendaria que cambiaran eso.
ResponderEliminarMe parecio muy bueno que pusieran las formulas porque asi es mas facil de apreciar y entender con mayor claridad todo.
Este blog esta muy completo, sus temas se pueden entender facilmente, a mi tambien me toco investigar sobre este tema, y creo que esta muy bien complementado! :D
ResponderEliminarAlejandra Moran 5B
muy bien el equipo, hizo buen trabajo con su tema, y las imagenes con movimientos de las ondas hizo mas entendible el tema me gusto, solo que por ahi venia un tema con material en ingles y pues la verdad no es muy comprendible, estaria bien que corrigieran eso :)
ResponderEliminarPero muy bien trabajo equipo :)
Muy interesante este blog me gusto mucho sus pagina y sus diagramas de tiempo son muy faciles de entender y acertivos nomas que cambielen tantito al color de fondo
ResponderEliminarluis Leyva 5B
muy buenos y claros ejemplos de las ondas en movimiento, solo que no entendi muy bien lo de elongación pero lo demas si esta claro buen trabajo compañeros
ResponderEliminarJESUS HIRAM GONZALEZ COVARRUBIAS
ResponderEliminarEl movimiento armónico simple: que queda descrito en función del tiempo por una función armónica seno o coseno. eso de nodo no lo entendi muy bien puesto que esta en ingles entre otras cosas pero en general muy bien expliado estos temas con ejemplos e imagenes.
buen trabajo equipo aunque estoy de acuerdo con mi compañero Ildefonsoque deberia de cambiar lo que pusieron en ingles pero todo lo demas me parecio mas y lo que mas me gusto fueron las imagenes que con ello queda un poco mas claro el tema y se puede logran una mejor compresiòn.
ResponderEliminarCinthya Blanco
estan muy bien las imagenes de las ondas y se comprenden facil pero si deberian de modificar esa explicion en engles.
ResponderEliminarcomo ya mis compañeros comentaron, esas explicaciones en ingles es lo unico que esta mal de ahi en fuera la informacion, con sus respectivas formulas e imagenes claras y muy entendibles, lo de elongacion no me quedo bastante claro pero es un buen trabajo
ResponderEliminarErik Vzla Quesney 5 B
Plebes muyy buuen trabajo verdaderamente los felicito!
ResponderEliminarBueno au poquito de mas informacion es lo de la frecuencia angular, es un muy buen tema las pulsaciones tambien las podemos llamar frecuencia angular,se refiere a la frecuencia del movimiento circular expresada en la proporción del cambio de ángulo, y se define como veces la frecuencia.
Estas son utilizadas en la pulsación en electricidad, electrónica, movimiento circular, movimiento ondulatorio, oscilaciones, osciladores, ondas, etc.
Dorle Elizabeth Meza Maldonado 5B
muy completo el tema con formulas y todo ..
ResponderEliminarlos temas no se me asen muy conocidos pero buena informacion
El tema anterior me parecio muy interesante, la forma en que estos interactuan y su manera de funcionar. Por otra parte el blog me parecio muy bueno ya que esta muy completo de información y se entiende super bien.
ResponderEliminarBuen trabajo :)
Lariza Armenta V.
bueno nose mucho de este tema pero ya me quedo mas claro,buenas imagenes y gracias por las formulas que dejan comprender un poco mejor el tema , en si buena informacion.
ResponderEliminarLuis Orduño
el tema de la ondas siempre va acompañado de la frecuencia, la frecuencia la vi en el tema del sonido , la informacion me parecio muy completa, lo unico que casi no se ve ademas hay material en ingles pero esta muy bien el blog
ResponderEliminarruben arana 5b
muy buen tema muy buen blog, informacion novedosa y me parecio interesante se puede represtentar con movimiento ondulatorio el del sonido. todos los temas van en armonia!
ResponderEliminaresta interesante el tema este, las ondas periodicas de los sonidos y los nodos, me parece interesante y completo por que te brindan informacion con formulas e imagenes muy bueno.
ResponderEliminarBrunet Arrazate 5b
un blog muy completo y bastabte interesante
ResponderEliminarlas ondas periodicas las cuales muestran periodos atravez del tiempo.
muchas felicidades es muy blog muy completo....
jeenifer flores 5b
pense que los nodos nomas eran de la electronicaaa pero noo ajajaja tambien se emplean en fisicaa.. esta chlo el tema y esta bien desarrollado pero ps ahi algunas partes en ingles y lo ubieran traducido antes de subirloo para que este mas entendiblee..
ResponderEliminarjesus abraham gastelum paredes ... 5B
completo el tema,exepto como dicen las partes e ingles, es bueno ver como lo que nosotros emos visto se emplea en estos temas y es mas facil entender,muy completo;)
ResponderEliminarAKAEMP EDUARDO MEZA