
Sobretonos armónicos.
Un sobretono es un componente senosoidal de la forma de una onda, de mayor frecuencia que su frecuencia fundamental. Generalmente el primer sobretono es el segundo armónico, el segundo sobretono el tercer armónico, etcétera.
Uso del término
Típicamente el término se refiere a ondas acústicas, especialmente en cuanto a temas relacionados a la música. A pesar del uso mezclado, un sobretono o es armónico o es parcial. El sobretono parcial o inarmónico es un múltiplo no entero de una frecuencia fundamental.
Un ejemplo de sobretonos armónicos:
| f | 440 Hz | tono fundamental | primer armónico |
| 2f | 880 Hz | primer sobretono | segundo armónico |
| 3f | 1320 Hz | segundo sobretono | tercer armónico |
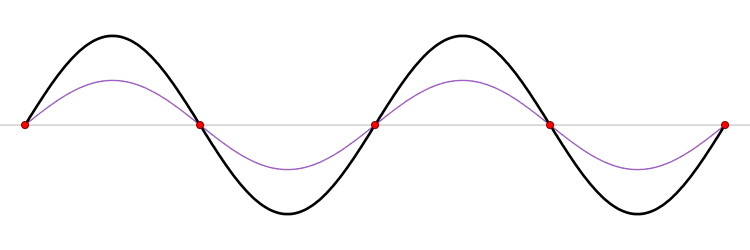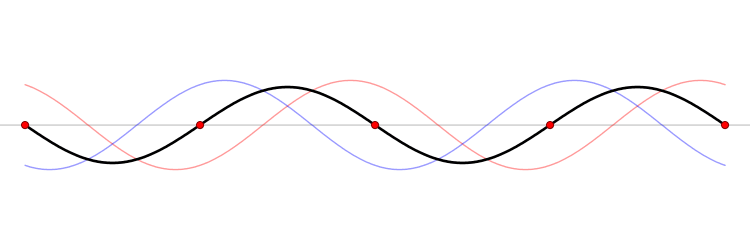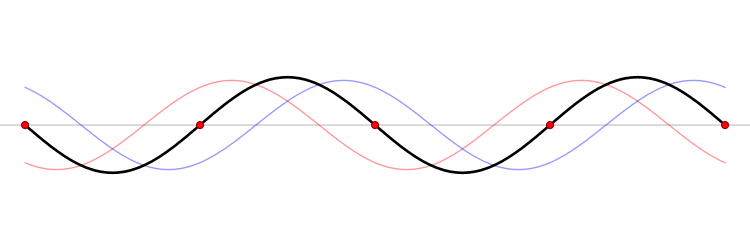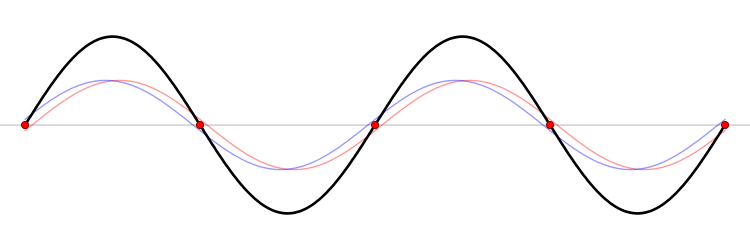
No todos los sobretonos son armónicos, o múltiplos enteros de la frecuencia fundamental. Algunos instrumentos musicales producen sobretonos más agudos o encerrados que los armónicos. Esta característica es uno de los varios elementos que aportan a su sonido.; como efecto secundario hace que las formas de onda no sean completamente periódicas.
Como la serie armónica es una secuencia aritmética (1f, 2f, 3f, 4f..), y la octava, o serie octava, es una secuencia geométrica (f, 2×f, 2×2×f, 2×2×2×f, ...), esto causa que el la serie de sobretonos divida la octava en partes más pequeñas según ascienda.
Movimiento armónico simple
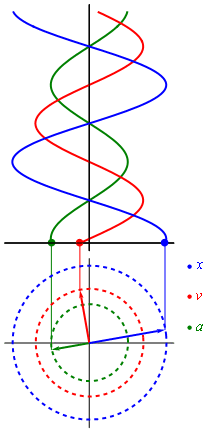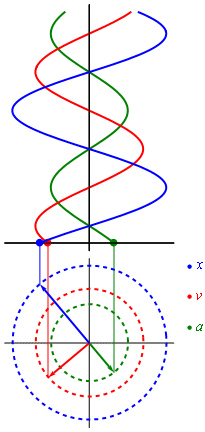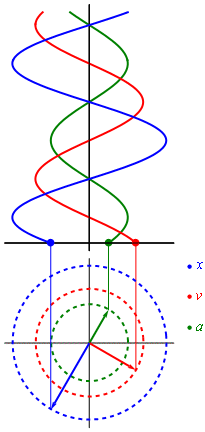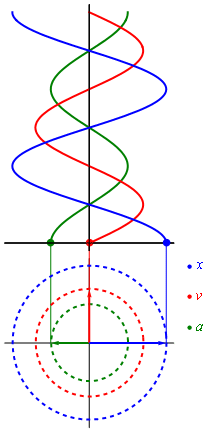
El movimiento armónico simple (se abrevia m.a.s.) es un movimiento periódico que queda descrito en función del tiempo por una función armónica (seno o coseno). Si la descripción de un movimiento requiriese más de una función armónica, en general sería un movimiento armónico, pero no un m.a.s..
En el caso de que la trayectoria sea rectilínea, la partícula que realiza un m.a.s. oscila alejándose y acercándose de un punto, situado en el centro de su trayectoria, de tal manera que su posición en función del tiempo con respecto a ese punto es una sinusoide. En este movimiento, la fuerza que actúa sobre la partícula es proporcional a su desplazamiento respecto a dicho punto y dirigida hacia éste.
Cinemática del movimiento armónico simple
El movimiento armónico simple es un movimiento periódico de vaivén, en el que un cuerpo oscila a un lado y a otro de su posición de equilibrio, en una dirección determinada, y en intervalos iguales de tiempo.
Por ejemplo, es el caso de un cuerpo colgado de un muelle oscilando arriba y abajo.El objeto oscila alrededor de la posición de equilibrio cuando se le separa de ella y se le deja en libertad. En este caso el cuerpo sube y baja.
Es también, el movimiento que realiza cada uno de los puntos de la cuerda de una guitarra cuando esta entra en vibración; pero, pongamos atención, no es el movimiento de la cuerda, sino el movimiento individual de cada uno de los puntos que podemos definir en la cuerda. El movimiento de la cuerda, un movimiento ondulatorio, es el resultado del movimiento global y simultáneo de todos los puntos de la cuerda.
Ecuación del movimiento
Elongación
En un movimiento armónico simple la magnitud de la fuerza ejercida sobre la partícula es directamente proporcional a su elongación, esto es la distancia  a la que se encuentra ésta respecto a su posición de equilibrio. En un desplazamiento a lo largo del eje Ox, tomando el origen O en la posición de equilibrio, esta fuerza es tal que
a la que se encuentra ésta respecto a su posición de equilibrio. En un desplazamiento a lo largo del eje Ox, tomando el origen O en la posición de equilibrio, esta fuerza es tal que  donde
donde  es una constante positiva y
es una constante positiva y  es la elongación. El signo negativo indica que en todo momento la fuerza que actúa sobre la partícula está dirigida hacía la posición de equilibrio; esto es, en sentido contrario a su elongación (la "atrae" hacia la posición de equilibrio).
es la elongación. El signo negativo indica que en todo momento la fuerza que actúa sobre la partícula está dirigida hacía la posición de equilibrio; esto es, en sentido contrario a su elongación (la "atrae" hacia la posición de equilibrio).
 a la que se encuentra ésta respecto a su posición de equilibrio. En un desplazamiento a lo largo del eje Ox, tomando el origen O en la posición de equilibrio, esta fuerza es tal que
a la que se encuentra ésta respecto a su posición de equilibrio. En un desplazamiento a lo largo del eje Ox, tomando el origen O en la posición de equilibrio, esta fuerza es tal que  donde
donde  es una constante positiva y
es una constante positiva y  es la elongación. El signo negativo indica que en todo momento la fuerza que actúa sobre la partícula está dirigida hacía la posición de equilibrio; esto es, en sentido contrario a su elongación (la "atrae" hacia la posición de equilibrio).
es la elongación. El signo negativo indica que en todo momento la fuerza que actúa sobre la partícula está dirigida hacía la posición de equilibrio; esto es, en sentido contrario a su elongación (la "atrae" hacia la posición de equilibrio).Aplicando la segunda ley de Newton, el movimiento armónico simple se define entonces en una dimensión mediante la ecuación diferencial
(1)
Siendo  la masa del cuerpo en desplazamiento. Escribiendo
la masa del cuerpo en desplazamiento. Escribiendo 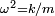 se obtiene la siguiente ecuación donde ω es la frecuencia angular del movimiento:
se obtiene la siguiente ecuación donde ω es la frecuencia angular del movimiento:
 la masa del cuerpo en desplazamiento. Escribiendo
la masa del cuerpo en desplazamiento. Escribiendo 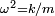 se obtiene la siguiente ecuación donde ω es la frecuencia angular del movimiento:
se obtiene la siguiente ecuación donde ω es la frecuencia angular del movimiento:(2)
La solución de la ecuación diferencial () puede escribirse en la forma
(3)
donde:
 es la elongación de la partícula.
es la elongación de la partícula. es la amplitud del movimiento (elongación máxima).
es la amplitud del movimiento (elongación máxima). es la frecuencia angular
es la frecuencia angular es el tiempo.
es el tiempo. es la fase inicial e indica el estado de oscilación o vibración (o fase) en el instante t = 0 de la partícula que oscila.
es la fase inicial e indica el estado de oscilación o vibración (o fase) en el instante t = 0 de la partícula que oscila.







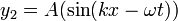


 y
y 









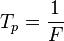 ,
,  es la frecuencia de la componente fundamental de la onda periódica y
es la frecuencia de la componente fundamental de la onda periódica y 
 es la amplitud de la sinusoide,
es la amplitud de la sinusoide, 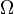 es la frecuencia en
es la frecuencia en 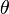 es la fase en radianes. En lugar de
es la fase en radianes. En lugar de  .
. y las constantes de fase
y las constantes de fase  , para una forma de onda dada se llama
, para una forma de onda dada se llama 
 el número total de armónicos de los que se compone la onda periódica. El armónico de frecuencia más baja se denomina primer armónico o armónico de frecuencia fundamental (
el número total de armónicos de los que se compone la onda periódica. El armónico de frecuencia más baja se denomina primer armónico o armónico de frecuencia fundamental ( , por tanto de amplitud
, por tanto de amplitud  , frecuencia
, frecuencia 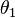 ). De hecho, el caso más simple, el de una onda armónica, es un caso particular para un único armónico (
). De hecho, el caso más simple, el de una onda armónica, es un caso particular para un único armónico ( ). Otros casos requieren un número infinito de armónicos que sólo pueden existir en sus formas perfectas como abstracciones matemáticas debido a que en la naturaleza no se pueden crear o transmitir señales de ancho de banda infinito. Sin embargo, incluso sus aproximaciones (descritos como la suma de un número limitado de armónicos) son de gran interés en la práctica, especialmente en Telecomunicaciones. Entre estos casos de señales periódicas compuestos por infinitos armónicos se encuentran las
). Otros casos requieren un número infinito de armónicos que sólo pueden existir en sus formas perfectas como abstracciones matemáticas debido a que en la naturaleza no se pueden crear o transmitir señales de ancho de banda infinito. Sin embargo, incluso sus aproximaciones (descritos como la suma de un número limitado de armónicos) son de gran interés en la práctica, especialmente en Telecomunicaciones. Entre estos casos de señales periódicas compuestos por infinitos armónicos se encuentran las ![x_a(t) = \frac {4A}{\pi} \sum_{n=1}^\infty \frac {1}{2n-1} \sin [(2n-1) \Omega t +\theta] \,\!](http://upload.wikimedia.org/math/c/2/9/c29b0e122721152e7d58af2f2996e638.png) ) o las
) o las 
![x_a(t) = \frac {4A}{\pi} \sum_{n=1}^{25} \frac {1}{2n-1} \sin [(2n-1) \Omega t +\pi] \,\!](http://upload.wikimedia.org/math/2/7/7/2770309267ccc66cd37eaa9d525de857.png)

 representa el desplazamiento periódico de una onda en una cierta posición. Si
representa el desplazamiento periódico de una onda en una cierta posición. Si 
